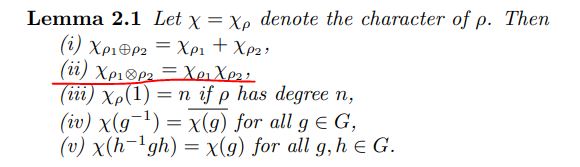一个群的共轭类与其不可约表示的数目相等。没理由没有对应关系啊。所以我一直在想有没有canonical的对应关系。现在终于想明白了 - 没有。这两个的关系是对偶关系 - 相当于线性空间与它的对偶空间之间的关系 - 没有canonical的对应关系 - 除非指定一个关系。
可以把这个类比写更清楚:
一方面以共轭类作基生成的线性空间,叫类空间吧。比如C1,C2,C3,C4,是4个共轭类。类空间是这样的:
λ1C1+λ2C2+λ3C3+λ4C4
另一方面,共轭类上的函数,叫类函数(class function),比如 f:
f(C1) = γ1
f(C2) = γ2
f(C3) = γ3
f(C4) = γ4
类空间和类函数空间 - 是对偶的吧?这就比较清楚了。
不可约表示相当于它的character,是一个类函数,属于类函数空间。所以不和类空间比如某个共轭类直接对应。
类空间有一个自然的基,{C1,C2,C3,C4},对应类函数空间的一个对偶基:就是某个类上取1,其他类取0。指定了这种对应关系,这两个空间就可以对应上了。
但这个对偶基在群表示论中很多时候不好用。要换基 - 取不可约表示的character作基。这个基再对偶回去到类空间,,,好像又不太好使了。
————
类函数空间换基的这个操作,也可以叫傅里叶变换。傅里叶变换抽象来看,就是一个线性空间换基的操作。
————
唯一存在的一个对应是:{e}共轭类对应trivial表示。但是和线性空间及其对偶空间的关系一样,在某些条件下对偶空间之间可以有对应关系。这个在李群中可能会更明显。因为李群的共轭类也是连续的。这是我觉得。我也不熟悉。
————
看群表示也是如此。先看类函数和representation之间的关系。
比如一个群G,有conjugacy class
Conj = {C1,C2,C3,C4}
Conj上的函数,就叫类函数。现在是4维。
另一方面,G有4个不可约表示:
Rep = {ρ1,ρ2,ρ3,ρ4}
还有4个对应的character:
Char = {α1,α2,α3,α4}
一个不可约character就是一个类函数,它相当于类函数空间上的另一套基。
傅里叶变换来了:
{f:Conj -> C} --> {f:Rep -> C}
{f:Rep -> C}和{f:Char -> C}是等价的。但是Char本身也是{f:Conj -> C}中的一个元素,所以有的时候会confuse。
这个傅里叶变换也有乘法到卷积,卷积到乘法。{f:Rep -> C} 那边的卷积不叫卷积,叫tensor product,但是内容是一样的。
————
这是看类函数。也可以看更大的群函数空间。{f: G -> C}。而类函数空间是它的子空间 - 如果两个群元素在同一个conjugacy class里,那么它们赋同样的值。
傅里叶变换怎么看成是基变换呢?这个有点难弄了。
群函数这边有“自然”的基:{δg},就是δ(g)=1,其他等于0。另一边是什么呢?另一边我们已经知道了,是matrix的直和。所以群函数这边的基就应该是这一套:
{g.α for g in G for α in Char}
g.α是g作用在α上,α是不可约表示的character,看成一个群函数。
这套数量看起来是 |G|*|Conj|,但是我们知道因为不可约表示的缘故,每一套作用都是限定在一个不变子空间中的。所以这里可以取出一套基来,而且每一套都是等价的。
傅里叶变换的另一边。是不可约方块的直和,也可以看成是matrix-valued function on Rep 或 Char。
卷积变乘法 - 这个是对的。
乘法变卷积 - 叫tensor product,应该也是对的。因为这是扩展定义,和类函数空间的定义compatible。我觉得。
————
哦。两个表示的tensor product,在character作为类函数这边变成了乘法。按照傅里叶变换把“乘法变为卷积,卷积变为乘法”的原则,tensor product这边应该可以叫卷积。不过这只是一个名字。